When it comes to geometry, shapes and their properties can be fascinating to explore. One such intriguing shape is a parallelogram. Parallelograms are quadrilateral shapes with opposite sides that are parallel and equal in length. Within this shape, there exist several important elements that play crucial roles in determining its properties. One such element is the diagonals of a parallelogram.
Understanding Parallelograms
Before delving into the concept of diagonals bisecting a parallelogram, let's first ensure a clear understanding of a parallelogram's basic properties.
Properties of a Parallelogram:
- Opposite sides are parallel: In a parallelogram, the opposite sides are parallel, meaning they will never intersect.
- Opposite sides are equal in length: The opposite sides of a parallelogram are also equal in length.
- Opposite angles are equal: The opposite angles within a parallelogram are of equal measure.
- Consecutive angles are supplementary: Consecutive (adjacent) angles in a parallelogram add up to 180 degrees.
Diagonals of a Parallelogram
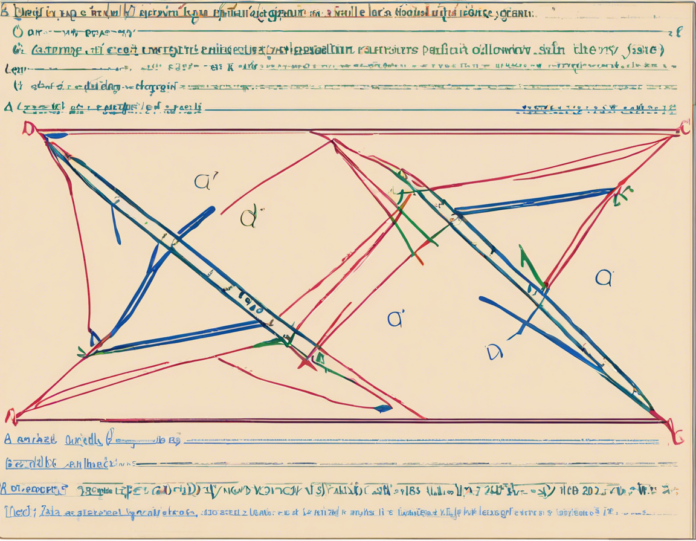
The diagonals of a parallelogram are the line segments that connect opposite vertices (corners) of the shape. In other words, they are the lines that run from one corner of the parallelogram to the corner opposite to it. These diagonals play a significant role in defining various properties of a parallelogram.
Properties of Diagonals in a Parallelogram:
- They bisect each other: This is the primary property we will focus on in this article. The diagonals of a parallelogram bisect each other, meaning they divide each other into two equal parts.
- They create congruent triangles: By drawing both diagonals, the parallelogram is divided into four triangles. These triangles formed by the diagonals are congruent (having the same size and shape) to each other.
- They form right angles: The diagonals of a parallelogram intersect at right angles. This property is crucial in various geometric calculations involving parallelograms.
Understanding Diagonals Bisecting a Parallelogram
Now, let's focus on the core aspect of this discussion: diagonals bisecting a parallelogram. This fundamental property states that the diagonals of a parallelogram divide each other into two equal parts.
To visualize this concept, consider a parallelogram ABCD. The diagonals AC and BD intersect at point O. In this scenario:
- Segment AO is equal in length to segment CO.
- Segment BO is equal in length to segment DO.
This property is consistent across all parallelograms, irrespective of their size or orientation. It remains constant as long as the shape maintains its fundamental characteristics.
Proof of Diagonals Bisecting a Parallelogram:
To understand why diagonals bisect a parallelogram, we can employ various geometric theorems and properties. One common approach is to utilize the concept of triangles and their properties. By considering the four triangles formed by the diagonals, we can establish the equality of their corresponding sides, ultimately proving that the diagonals bisect each other.
Applications of Diagonals Bisecting a Parallelogram
The property of diagonals bisecting a parallelogram finds applications in various mathematical and practical scenarios. Some of these applications include:
- Calculating geometric properties: Knowing that the diagonals bisect each other aids in determining other aspects of the parallelogram, such as angles and side lengths.
- Constructing perpendicular lines: The fact that the diagonals intersect at right angles can be useful when constructing perpendicular lines or right angles in geometric constructions.
- Problem-solving in geometry: Understanding this property can simplify problem-solving tasks that involve parallelograms, enabling quicker and more accurate solutions.
FAQs (Frequently Asked Questions)
Q1: Why do diagonals bisect a parallelogram?
A1: Diagonals bisect a parallelogram due to the geometric properties of triangles formed by the diagonals. Through triangle congruence principles, it can be proved that the diagonals divide each other into two equal segments.
Q2: Do all parallelograms have bisecting diagonals?
A2: Yes, all parallelograms have bisecting diagonals. This property is inherent to the nature of parallelograms and is consistent across all instances of this geometric shape.
Q3: How does the property of bisecting diagonals help in identifying a parallelogram?
A3: The presence of bisecting diagonals is a key characteristic of parallelograms. When observing a quadrilateral with diagonals that divide each other equally, it indicates that the shape is a parallelogram.
Q4: Can a shape with bisecting diagonals always be considered a parallelogram?
A4: No, a shape with bisecting diagonals does not always qualify as a parallelogram. Other properties of a parallelogram, such as parallel sides and equal angles, must also be present for it to be classified as such.
Q5: How can one prove that the diagonals of a parallelogram bisect each other?
A5: The proof typically involves utilizing triangle congruence theorems and properties. By demonstrating that the triangles formed by the diagonals are congruent, one can show that the diagonals bisect each other.
In conclusion, the property of diagonals bisecting a parallelogram is a fundamental aspect of the geometric nature of parallelograms. Understanding this property not only enhances one's knowledge of geometry but also provides valuable insights for solving geometric problems and applications.